AI Decision-making & Pathfinding in Games

Game Development 101: (incomplete)
a. Basics of Game Development
b. Designing your Video Game
c. Math in Video Games
d. AI Decision-making & Pathfinding
e. Asset Creation & Game Art
f. Physics & Collision Detection
g. Shaders & VFX in Games
h. Multiplayer & Networking in Games

Table of Contents

Path finding Techniques

Most games require AI to travel to some place; as in chasing the player intelligently or just driving along the roads to some place. For this, we need an algorithm. The algorithm we will use is called A* (read A-star). it is the most common approach used in most video games.

Overview of A* Algorithm

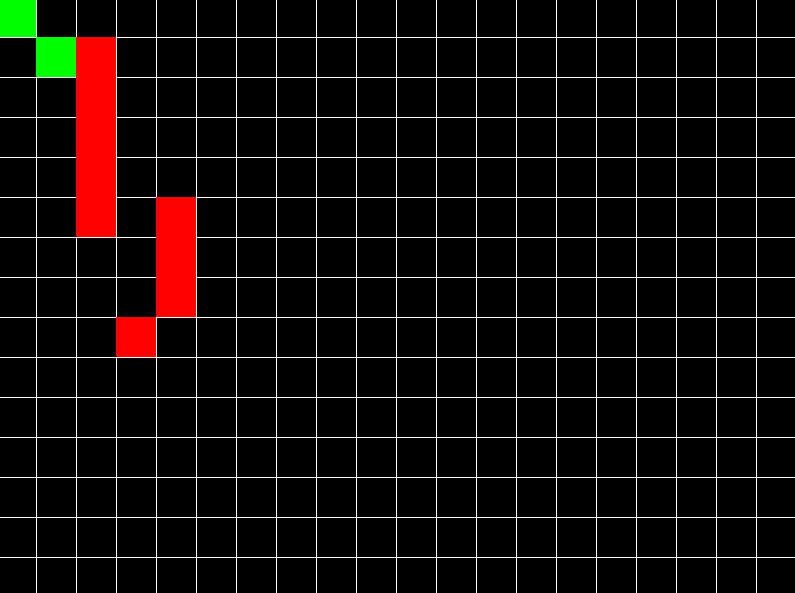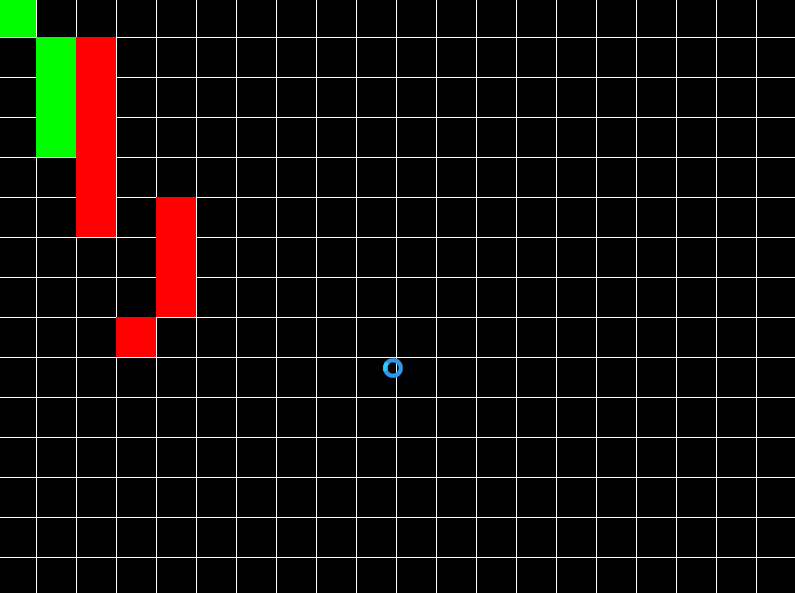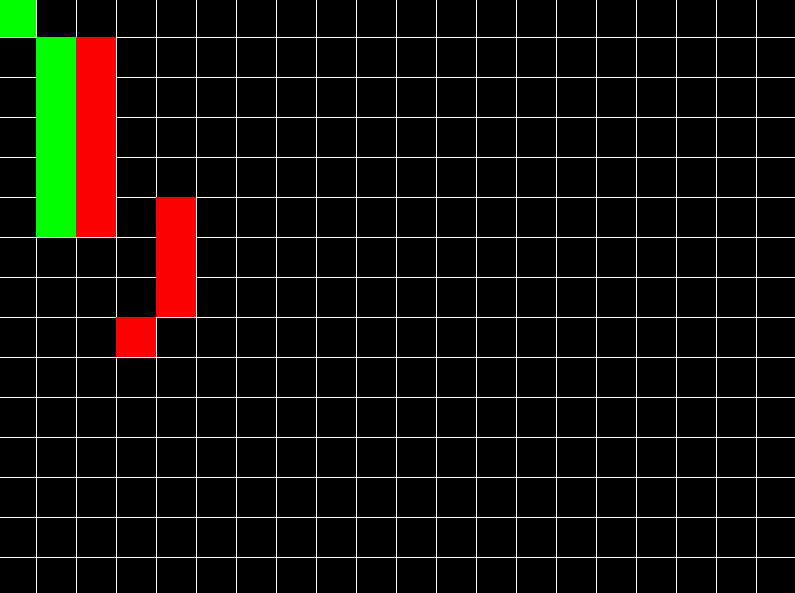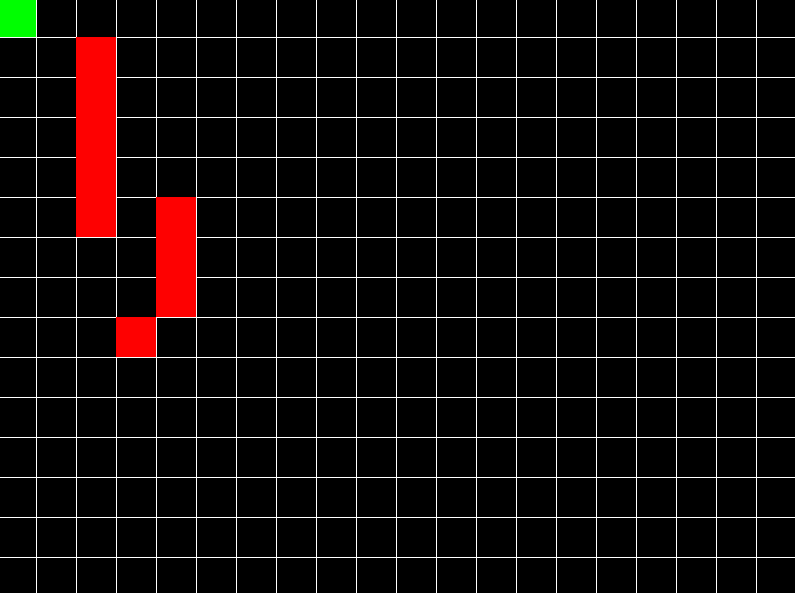
A* takes graph data structure as its input along with the source & destination nodes where we wish to go. It then traverses the graph & tries to reach the destination node by following path that takes less cost/distance.
Whenever it encounters a node with multiple paths leading to it; it checks which one took less cost & selects it as the most efficient so far; until the better one is found. Also, it makes use of a value called ‘heuristic’, which is just an estimate of total distance. In a sense, heuristic is like the overall ‘feel’ that makes a particular path seem more efficient, so algorithm proceeds towards the direction guided by this heuristic value. A direct line joining current node & the destination node could be a heuristic as well.

The working of A* is discussed in this post in detail; here we will focus only on the implementation.

Working & Pseudocode of A*

A* can only work on graphs. So we first convert our 2D space into a graph structure. For this we make a grid & all the vertices of grid are nodes & there are 4 edges connecting each node with 4 neighbors (though you can make 8 edges as well, depends on your choice). After getting a graph structure, we apply the algorithm on it to compute the path. The path is finally traced by traversing parent attribute in nodes. The following is pseudocode in C-like syntax:

// Define a structure for a node
struct Node {
    // Properties of a node
    // For example, assuming each node has x, y coordinates, g, h, and f scores
    int x, y;
    float g, h, f; // g: cost from start, h: heuristic cost to goal, f: g + h
    struct Node* parent; // pointer to the parent node
};

// Function to perform A* search
void AStarSearch(struct Node* start, struct Node* destination) {
    // Create open and closed lists
    // Assuming these are linked lists or any other appropriate data structures
    struct NodeList* openList = createEmptyList();
    struct NodeList* closedList = createEmptyList();

    // Add the starting node to the open list
    addNodeToList(openList, start);

    // While destination node has not been reached
    while (!isDestinationReached(openList, destination)) {
        // Consider the node with the lowest f score in the open list
        struct Node* current = getNodeWithLowestFScore(openList);

        // If this node is our destination node, we are finished
        if (current == destination) {
            // Destination reached, perform any necessary actions
            break;
        }

        // Put the current node in the closed list and look at its neighbors
        removeNodeFromList(openList, current);
        addNodeToList(closedList, current);

        // For each neighbor of the current node
        for (int i = 0; i < current->numNeighbors; i++) {
            struct Node* neighbor = current->neighbors[i];

            // Check conditions for updating g values and parents
            if (neighbor->g > current->g + distance(current, neighbor) && isInList(closedList, neighbor)) {
                neighbor->g = current->g + distance(current, neighbor);
                neighbor->parent = current;
            } else if (current->g + distance(current, neighbor) < neighbor->g && isInList(openList, neighbor)) {
                neighbor->g = current->g + distance(current, neighbor);
                neighbor->parent = current;
            } else if (!isInList(openList, neighbor) && !isInList(closedList, neighbor)) {
                addNodeToList(openList, neighbor);
                neighbor->g = current->g + distance(current, neighbor);
                neighbor->parent = current;
            }
        }
    }

    // Perform any necessary actions after reaching the destination
}

Bellman-Ford Equation makes it easy to understand how we update path in a graph when we find better one:

distance[v] = min(distance[v], distance[u] + weight(u,v))

* distance[v] is current distance to node v

* distance[u] is distance to u, which is neighbor of node v

* weight(u,v) is the distance between u & v (the edge weight)

The algorithm selects the distance that is minimum among the two possible choices (either the current distance is already better then path through node u or not).

Implementing A* in 2D World

In following implementation, 2D space is discretized & all except those points which are marked as ‘obstacles’ are searched. It means, if we have some obstacle, we can just pass all the points contained by that object in obstacles list. The simple code in PyGame is following, if you just want to port it to your target engine, just focus only on astar_continous():

# Author: Mujtaba
# Date: Jan 30, 2024

# Description: Game-ready version of A* algorithm in 2D. It only requires start/end points and
# points to avoid (obstacles). Does not create a heavy graph structure explicitly (which is
# memory-inefficient for large game worlds).

import pygame
import heapq
import sys

# Constants for visualization
WIDTH, HEIGHT = 800, 600
CELL_SIZE = 40

def heuristic(node, goal):
    # Euclidean distance heuristic
    return ((node[0] - goal[0]) ** 2 + (node[1] - goal[1]) ** 2) ** 0.5

def astar_continuous(start, goal, obstacles=[]):
    unvisited = [(heuristic(start, goal), start)]
    visited = set()
    previous = {start: None}
    cost_so_far = {start: 0}

    while unvisited:
        current_cost, current_node = heapq.heappop(unvisited)

        if current_node == goal:
            path = []
            while current_node is not None:
                path.append(current_node)
                current_node = previous[current_node]
            return path[::-1]

        visited.add(current_node)

        neighbors = [
            # adjacent neighbors (left, right, up, down)
            (current_node[0] + 1, current_node[1]),
            (current_node[0] - 1, current_node[1]),
            (current_node[0], current_node[1] + 1),
            (current_node[0], current_node[1] - 1),
            # diagonal neighbors (top-left, top-right, bottom-left, bottom-right)
            (current_node[0] + 1, current_node[1] + 1),
            (current_node[0] - 1, current_node[1] - 1),
            (current_node[0] + 1, current_node[1] - 1),
            (current_node[0] - 1, current_node[1] + 1)
        ]

        for neighbor in neighbors:
            if neighbor not in obstacles:
                new_cost = cost_so_far[current_node] + 1

                if neighbor not in visited or new_cost < cost_so_far.get(neighbor, float('inf')):
                    cost_so_far[neighbor] = new_cost
                    priority = new_cost + heuristic(neighbor, goal)
                    heapq.heappush(unvisited, (priority, neighbor))
                    previous[neighbor] = current_node

    return None  # No path found

## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ##
## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ##

## Testing in pygame ##

def draw_grid(screen):
    for x in range(0, WIDTH, CELL_SIZE):
        pygame.draw.line(screen, (255, 255, 255), (x, 0), (x, HEIGHT))
    for y in range(0, HEIGHT, CELL_SIZE):
        pygame.draw.line(screen, (255, 255, 255), (0, y), (WIDTH, y))

def draw_obstacles(screen, obstacles):
    for obstacle in obstacles:
        pygame.draw.rect(screen, (255, 0, 0), (obstacle[0] * CELL_SIZE, obstacle[1] * CELL_SIZE, CELL_SIZE, CELL_SIZE))

def draw_path(screen, path):
    for node in path:
        pygame.draw.rect(screen, (0, 255, 0), (node[0] * CELL_SIZE, node[1] * CELL_SIZE, CELL_SIZE, CELL_SIZE))
        pygame.display.flip()
        pygame.time.wait(200)

def main():
    pygame.init()
    screen = pygame.display.set_mode((WIDTH, HEIGHT))
    pygame.display.set_caption("A* Algorithm Visualization")

    start_point = (0, 0)
    goal_point = (4, 8)
    obstacles = [(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (4, 5), (4, 6), (4, 7), (3, 8)]

    path = astar_continuous(start_point, goal_point, obstacles)

    if path:
        print("Path found:", path)
    else:
        print("No path found.")

    while True:
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                pygame.quit()
                sys.exit()

        screen.fill((0, 0, 0))
        draw_grid(screen)
        draw_obstacles(screen, obstacles)
        draw_path(screen, path)

        pygame.display.flip()

if __name__ == "__main__":
    main()

Excluding vertices that are ‘inside’ an obstacle

Above implementation does avoid the obstacles, but how exactly should we pass obstacles for large worlds? The answer is, we can use some function to fill obstacles array. The pseudocode to that function could look like:

def fill_obstacles():
    for each point (x, y) within 2d world bounds:
        if that point lies within any of the Area2Ds marked as obstacles:
            obstacles.add(vec2(x, y))

For static geometry, this calculation can be done before main game loop to save performance. For dynamic objects, we can make another obstacle array called dynamic_obstacles[] and compute its values per frame. The a-star algorithm function will then be slightly modified to ignore the point if it lies within either obstacles[] or dynamic_obstacles[].

Decision-making Techniques

We can use multiple techniques such as finite-state machines, decision trees or behavior trees.

Decision Trees

Decision tree is a simple tree data structure; where all the nodes except the leaf nodes are conditions & the leaf nodes are the actions that must be taken if particular branch of conditions are met. It is just another fancier way to have nested if-else. Just not hardcoded.

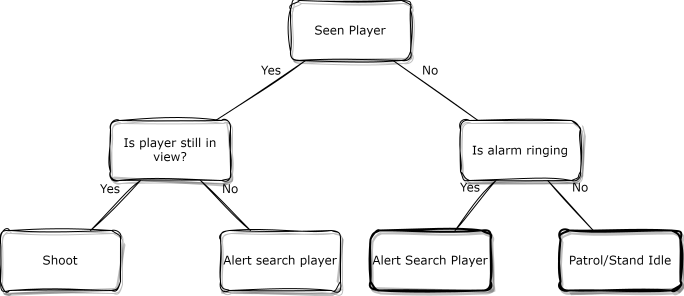
Finite State Machines

Finite state machines is a concept in which we have some initial state of our AI entity & there are certain states it can transit to. For example, it can remain in idle state, patrolling the area, but whenever it sees a player, it transits to alerted state & the action corresponding to this alerted state will be the path finding to player if player is hidden or if player is in clear sight (another state), then shoot the player.

gameidea