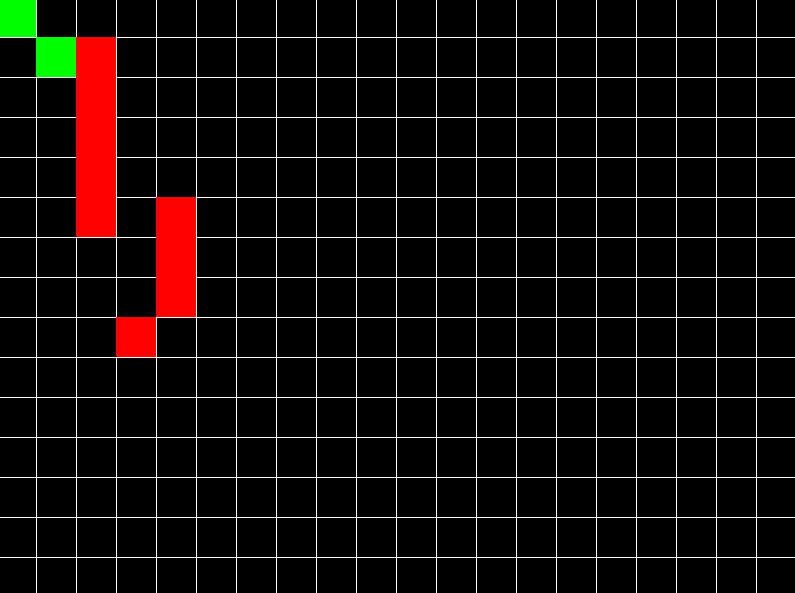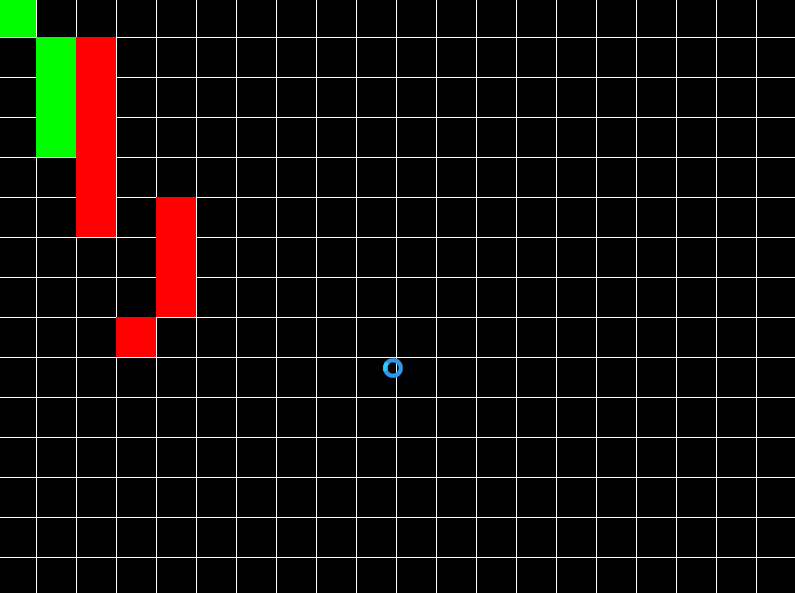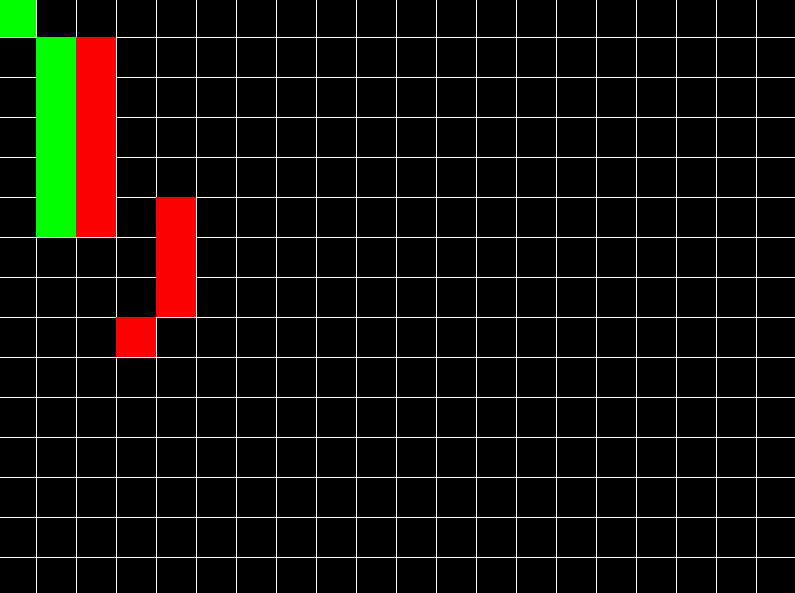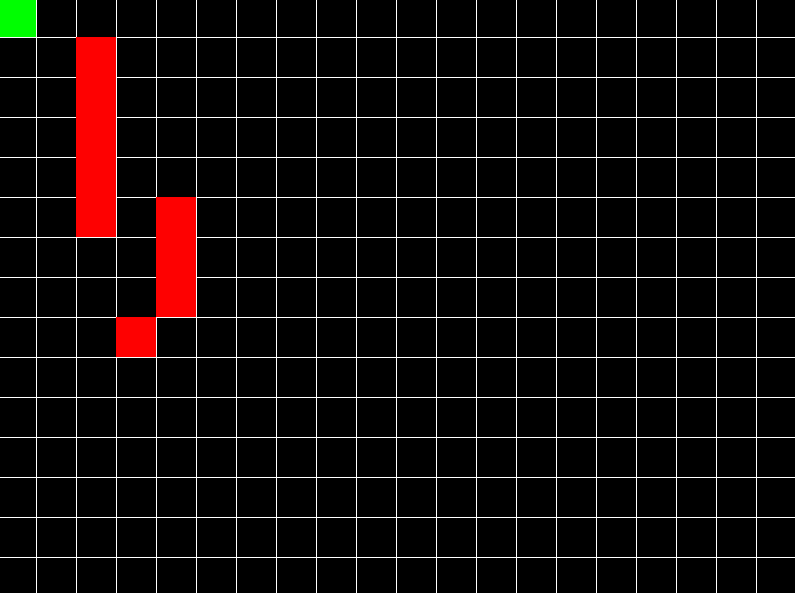
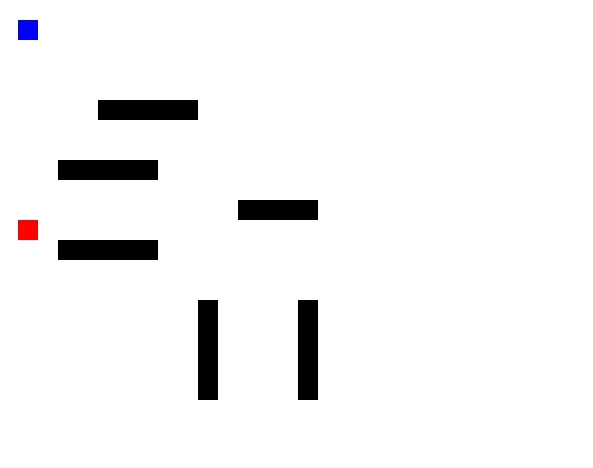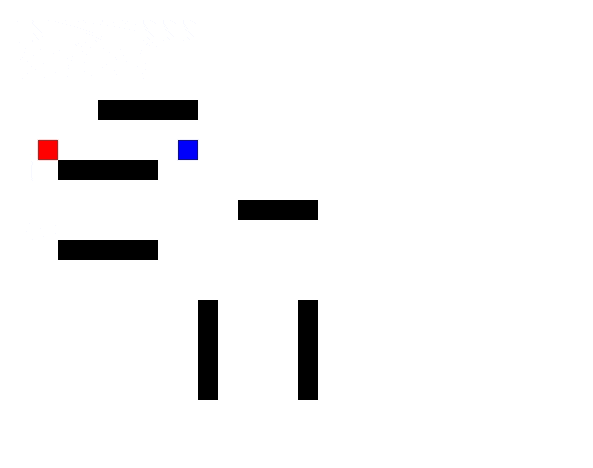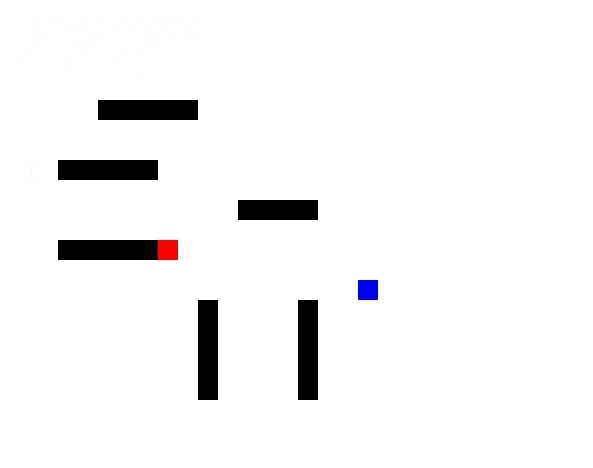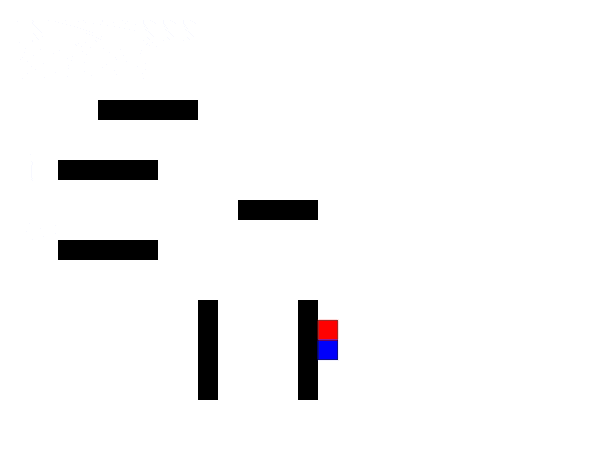Red enemy chasing the player using A* algorithm, avoiding obstacles. GitHub link.

You want your enemy to take the shortest path to the player in your game. You are aware of graph data structure & want to use it to represent the 2D world. Then you will apply this algorithm on the graph & use the algorithm’s output to move the enemy on the right path. It is one of the most useful algorithms while making video games.

What is a Graph?

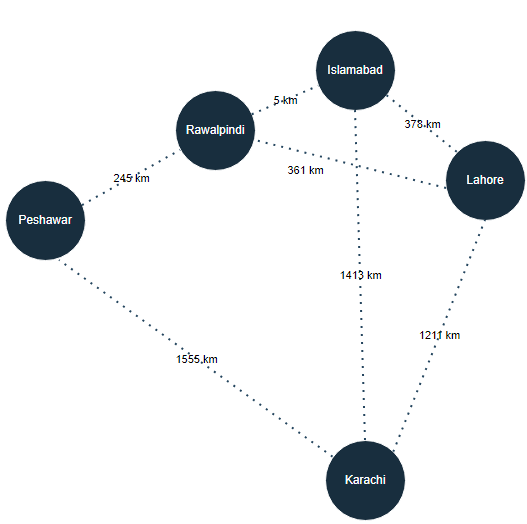
You have cities & roads connecting them. You have individual people, and those people are friends to many other people. These type of things can be represented as a graph. In graph, we have some entities (can be any type), and we have relationships among those entities. In diagrams, we represent them as nodes and edges connecting those nodes; like this:

In a Nutshell

A* algorithm for finding shortest path is, in simple words same as Dijkstra algorithm with a slight difference. In dijkstra, the algorithm considers edge cost only to determine which node to jump next. In A* however, the algorithm also considers (in addition to edge cost) an estimated value of cost from current node to the final destination. So in A* algorithm, (C + E) is used to decide which node to jump next, where C is edge cost & E is estimation (we call it heuristic value). In Dijkstra’s algorithm, only C is used to decide which node to jump next. If you set E to be zero for all nodes, A* becomes Dijkstra.

If you haven’t yet understood Dijkstra’s algorithm, I highly recommend reading it since A* is a variant of Dijkstra. Thus a small part of Dijkstra algorithm is modified to add more efficiency & we call it A* algorithm.

Getting Started with A* Algorithm

Since it is a graph traversal algorithm, we need a graph to feed into it as input. The easiest way to make a graph is to assume that your 2D space is a grid. Each point in a grid is a vertex (or node) and each vertex has 4 edges connecting to it. Assume that our source vertex is vec2(0, 0) which is origin of 2D space. And assume any destination point where you want to go (for example vec2(x, y)).

Now with the above assumption, we start the algorithm’s process. Initially, we set distance to our source node as 0 & all other nodes as infinity. Now we iterate the set of all unvisited nodes & get the node with smallest value of cost + heuristic (C + E). And we jump to that node. After jumping, we immediately update its distance from source to be equal to cost (and no longer infinity). Now we remove the node from unvisited list & continue the process till destination is reached.

What exactly is a heuristic?

What exactly is meant by the “estimated distance from current node to destination”? It can be calculated by any of the below methods.

1. Euclidean Distance: This is the direct vector or straight-line between the current node and the final destination node. It is calculated using the geometric distance formula, often referred to as the Euclidean distance formula, which considers the length of the straight line connecting the two points.

E = sqrt ((current_node.x – destination_node.x)^2 + (current_node.y – destination_node.y)^2)

2. Manhattan Distance: It is calculated as the sum of the absolute differences between the x-coordinates and y-coordinates of the current node and the destination.

E = abs (current_node.x – destination_node.x) + abs (current_node.y – destination_node.y)

3. More methods: In a video game, there can be many other factors that you can add to heuristic to influence the pathfinding process. It can be adding some weights to dangerous areas so peaceful creatures should avoid it, and so on.

Pseudo-code

function AStar(source, destination):
    unvisited = [source]
    visited = []

    while unvisited is not empty:
        current = node with the lowest total cost in unvisited

        if current is destination:
            return reconstructPath(current)

        remove current from unvisited
        add current to visited

        for each neighbor of current:
            if neighbor is in visited:
                continue

            tentativeCost = current.cost + distance(current, neighbor) + heuristic(neighbor, destination)

            if neighbor is not in unvisited or tentativeCost < neighbor.cost:
                neighbor.cost = tentativeCost
                neighbor.previous = current

                if neighbor is not in unvisited:
                    add neighbor to unvisited

    return failure

In above pseudocode, previous pointer is used to trace the path back to source in reconstructPath() function.

Python Implementation

import heapq

def heuristic(node, goal):
    # Euclidean distance heuristic
    return ((node[0] - goal[0]) ** 2 + (node[1] - goal[1]) ** 2) ** 0.5

def astar_continuous(start, goal, obstacles=[]):
    unvisited = [(heuristic(start, goal), start)]
    visited = set()
    previous = {start: None}
    cost_so_far = {start: 0}

    while unvisited:
        current_cost, current_node = heapq.heappop(unvisited)

        if current_node == goal:
            path = []
            while current_node is not None:
                path.append(current_node)
                current_node = previous[current_node]
            return path[::-1]

        visited.add(current_node)

        neighbors = [
            (current_node[0] + 1, current_node[1]),
            (current_node[0] - 1, current_node[1]),
            (current_node[0], current_node[1] + 1),
            (current_node[0], current_node[1] - 1),
        ]

        for neighbor in neighbors:
            if neighbor not in obstacles:
                new_cost = cost_so_far[current_node] + 1

                if neighbor not in visited or new_cost < cost_so_far.get(neighbor, float('inf')):
                    cost_so_far[neighbor] = new_cost
                    priority = new_cost + heuristic(neighbor, goal)
                    heapq.heappush(unvisited, (priority, neighbor))
                    previous[neighbor] = current_node

    return None  # No path found

# Example usage:
start_point = (0, 0)
goal_point = (4, 4)

path = astar_continuous(start_point, goal_point)

if path:
    print("Path found:", path)
else:
    print("No path found.")

More

1. You can visualize different path finding & search algorithms here.