You have created a graph data structure. Now you want to search for an element within it. The simplest algorithm could be DFS. Depth First Search (DFS) is a searching algorithm that searches the graph for our given data. Graph search algorithms cannot jump to any node; they must move through the edges (connectors) between the nodes in order to explore the graph.
Graph is a structure in which you create objects to store data, and then link those objects. For example, you have a town which you want to represent in a computer. You will create objects for buildings and link some of the buildings (which in real life are connected by roads). The visualization of such a graph could be like this:
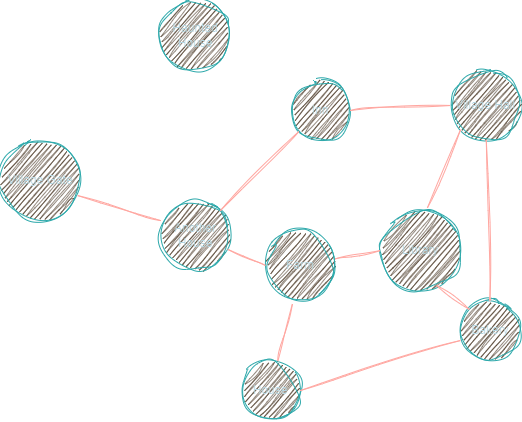
DFS Algorithm
Depth First Search (DFS) selects a branch in a graph, and dives deep into it, until it reaches its end. After that, it backtracks (comes back to the origin) and then selects the next branch to deep dive into. This process is repeated until all the graph is explored.
This is opposite to breadth first search, where we explore the nodes at the same level before exploring their children at the next levels.

Depth first search applies to trees as trees are a type of graph.
Where do we use Depth First Search?
This algorithm is fundamentally a simple searching algorithm for simpler graphs. They are useful for problems such as:
- Making a Maze game and searching for its solution.
- In chess or tic-tac-toe game AI player. A variant of DFS, called Minimax algorithm is used for chess and tic-tac-toe.
- In a websites crawling and scraping program, where DFS keeps following all the links to a webpage, and then follows more links in those linked web pages and so on. Until it forms a huge graph of linked websites.


Is DFS the best algorithm for searching?
In very simple cases, such as when a graph is small and has no additional information other than data and links between data, DFS can be the best algorithm. However, as we scale the system, DFS becomes sub-optimal or useless ins some cases.
- For problems such as route calculation, there could be many paths that lead to same destination. If we employed DFS, it will select the first turn & keep exploring it, no matter how far it reaches. This is extremely in-efficient. So we employ algorithms such as Dijkstra or A-star.
- If in maze or puzzle solving, there are multiple paths, and one of them is better, the DFS will not be able to distinguish. So to calculate the better path, we again go for A-star.
Implementing DFS algorithm
DFS explores as far down a path as possible before backtracking, which means it “dives deep” into the graph structure before switching branches. DFS can be implemented using either recursion or a stack data structure.
DFS Process
- Create a set called
visitedto store all the nodes which are explored (initially empty). - Create a stack and add the starting node to it.
- Loop over the stack, until it gets empty. In each loop cycle do:
- Pop the node from stack.
- Process the node (by default print or do nothing).
- Add the node to visited.
- Put all the node’s neighbors to stack for the successive cycles to process.
- When all the nodes will be explored in graph, stack will eventually get empty and algorithm will return.
Python code for DFS using stack:
def dfs(graph, start):
visited = set()
stack = [start]
while stack:
vertex = stack.pop()
if vertex not in visited:
visited.add(vertex)
# Add all unvisited neighbors to the stack
stack.extend(neighbor for neighbor in graph[vertex] if neighbor not in visited)
return visitedWhy we use Stack in DFS?
In stack, the freshly added neighboring nodes (which are the children of current node) will be popped out immediately in next cycle. And those added earlier will get pushed down and down as more children and grand-children nodes are added. Thus stack allows the algorithm to explore the children nodes first, which cause it to dive deeper.
If we used queue, the nodes which came to the queue first, the siblings of current nodes, will get processed first before the children (which are added at end end of the queue) will be processed. This is the key difference between DFS and BFS. BFS uses queue instead of stack.
Making a maze in Python
We will make a test maze in python using 2D arrays:
# 0 - open path, 1 - wall
maze = [
[0, 1, 0, 0, 0],
[0, 1, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0]
]
start = (0, 0) # Start at the top-left corner
end = (4, 4) # End at the bottom-right cornerNow we have to convert this 2D maze representation to a graph data structure. In graph, we will connect all the open paths into edges, so algorithm will be able to traverse them. And walls will not be connected in graph so algorithm will not be able to traverse them. Coverting maze into a graph in Python:
# Convert the maze to a graph representation
def maze_to_graph(maze):
graph = {}
rows, cols = len(maze), len(maze[0])
for i in range(rows):
for j in range(cols):
if maze[i][j] == 0: # only consider open paths
graph[(i, j)] = []
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]: # neighbors (up, down, left, right)
nx, ny = i + dx, j + dy
if 0 <= nx < rows and 0 <= ny < cols and maze[nx][ny] == 0:
graph[(i, j)].append((nx, ny))
return graph
# Convert maze to graph
graph = maze_to_graph(maze)Now that we made the graph from maze. We will simply apply DFS to check the solution.
# Check if there is a path from start to end
visited_nodes = dfs(graph, start)
if end in visited_nodes:
print("Maze is solved!!")
print(visited_nodes)
else:
print("Maze unsolvable.")
Converting into a better maze game
The above test is a simple example. To covert it into a good maze game, you can use python graphics libraries to visualize the 2D maze representation in graphics form. PyGame is one example. Below is Pygame-based visualization of above Maze problem that we solved using DFS:
import pygame
import time
# Initialize Pygame
pygame.init()
# Constants
SCREEN_WIDTH = 500
SCREEN_HEIGHT = 500
CELL_SIZE = 100
WHITE = (255, 255, 255)
BLACK = (0, 0, 0)
RED = (255, 0, 0)
GREEN = (0, 255, 0)
# Set up the display
screen = pygame.display.set_mode((SCREEN_WIDTH, SCREEN_HEIGHT))
pygame.display.set_caption("DFS Maze Solver")
# Maze example
maze = [
[0, 1, 0, 0, 0],
[0, 1, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0]
]
start = (0, 0)
end = (4, 4)
# Convert the maze to a graph representation
def maze_to_graph(maze):
graph = {}
rows, cols = len(maze), len(maze[0])
for i in range(rows):
for j in range(cols):
if maze[i][j] == 0:
graph[(i, j)] = []
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
nx, ny = i + dx, j + dy
if 0 <= nx < rows and 0 <= ny < cols and maze[nx][ny] == 0:
graph[(i, j)].append((nx, ny))
return graph
# DFS algorithm
def dfs(graph, start):
visited = set()
stack = [start]
path = []
while stack:
vertex = stack.pop()
if vertex not in visited:
visited.add(vertex)
path.append(vertex)
# Visualization
screen.fill(WHITE)
draw_maze(maze, path)
pygame.display.flip()
time.sleep(0.5) # pause to visualize
stack.extend(neighbor for neighbor in graph[vertex] if neighbor not in visited)
return path
# Draw the maze
def draw_maze(maze, path):
rows, cols = len(maze), len(maze[0])
for i in range(rows):
for j in range(cols):
color = WHITE if maze[i][j] == 0 else BLACK
pygame.draw.rect(screen, color, (j * CELL_SIZE, i * CELL_SIZE, CELL_SIZE, CELL_SIZE))
for (x, y) in path:
pygame.draw.rect(screen, RED, (y * CELL_SIZE, x * CELL_SIZE, CELL_SIZE, CELL_SIZE))
pygame.draw.rect(screen, GREEN, (start[1] * CELL_SIZE, start[0] * CELL_SIZE, CELL_SIZE, CELL_SIZE))
pygame.draw.rect(screen, GREEN, (end[1] * CELL_SIZE, end[0] * CELL_SIZE, CELL_SIZE, CELL_SIZE))
# Main function
def main():
graph = maze_to_graph(maze)
dfs(graph, start)
running = True
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
screen.fill(WHITE)
draw_maze(maze, [])
pygame.display.flip()
pygame.quit()
if __name__ == "__main__":
main()
Thank you for reading <3
