Perlin noise is a type of continuous, smooth noise that helps to generate visually cohesive and random-looking patterns. Unlike traditional random noise & value noise, Perlin noise produces “coherent” noise, meaning nearby points have similar values. This gives the resulting pattern a naturally flowing appearance, similar to textures you would find in nature, such as clouds, terrain, and wood grains.

Why Perlin Noise is Different

Instead of using purely random values, Perlin noise uses gradients at each point, which are interpolated smoothly across the noise space. This produces smooth transitions and avoids the “static” look of purely random noise. This makes it ideal for procedural generation in digital art, video games, and simulations.

Okay, but why it is different then Value noise? Because value noise look blocky & unrealistic, although it is similar to Perlin in having gradients.

Use Cases of Perlin Noise

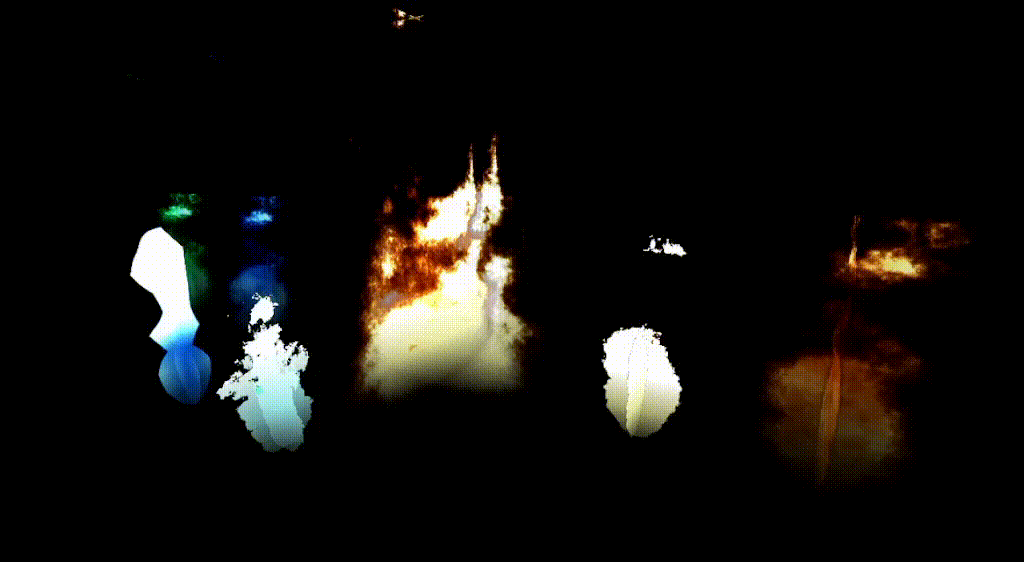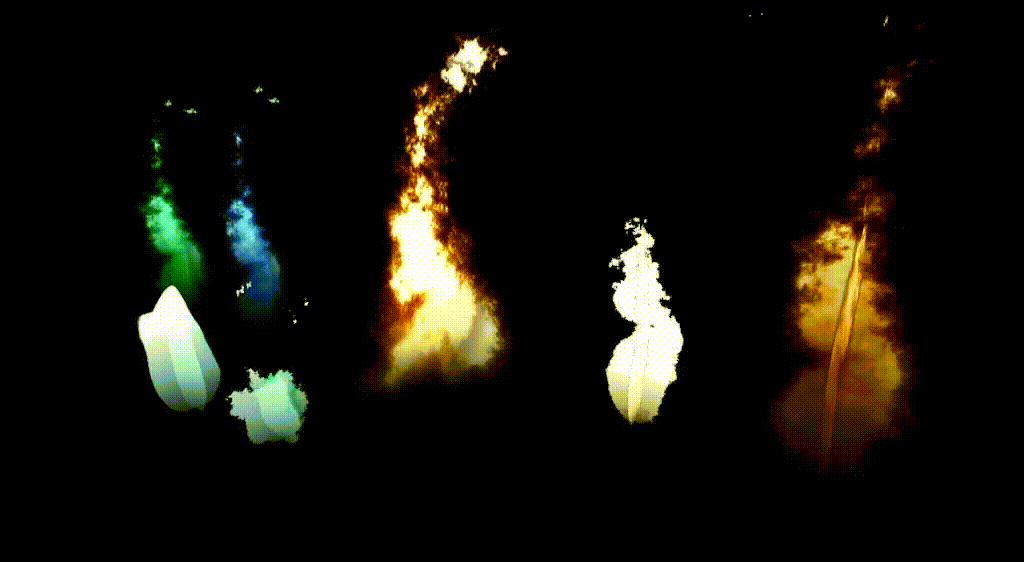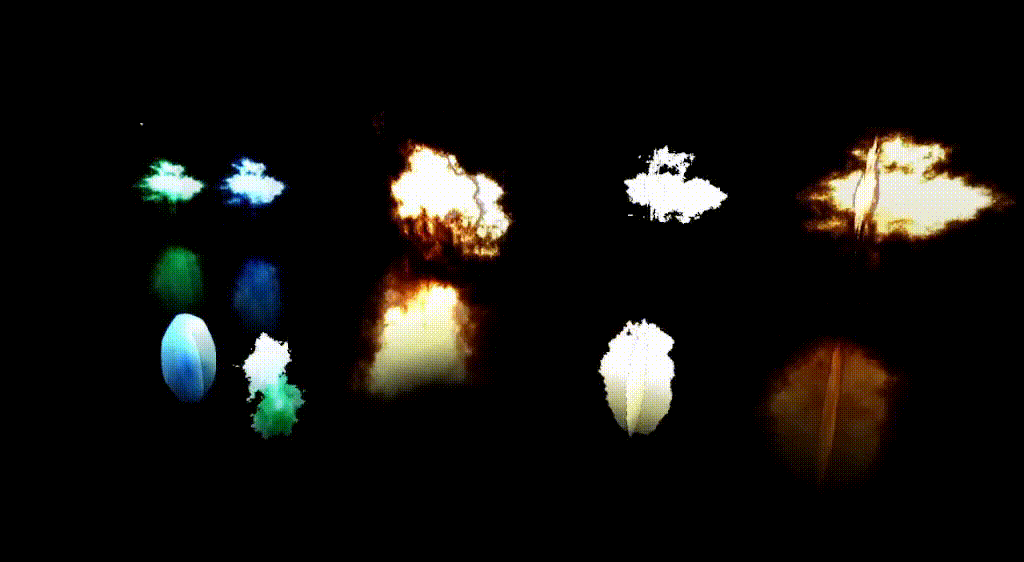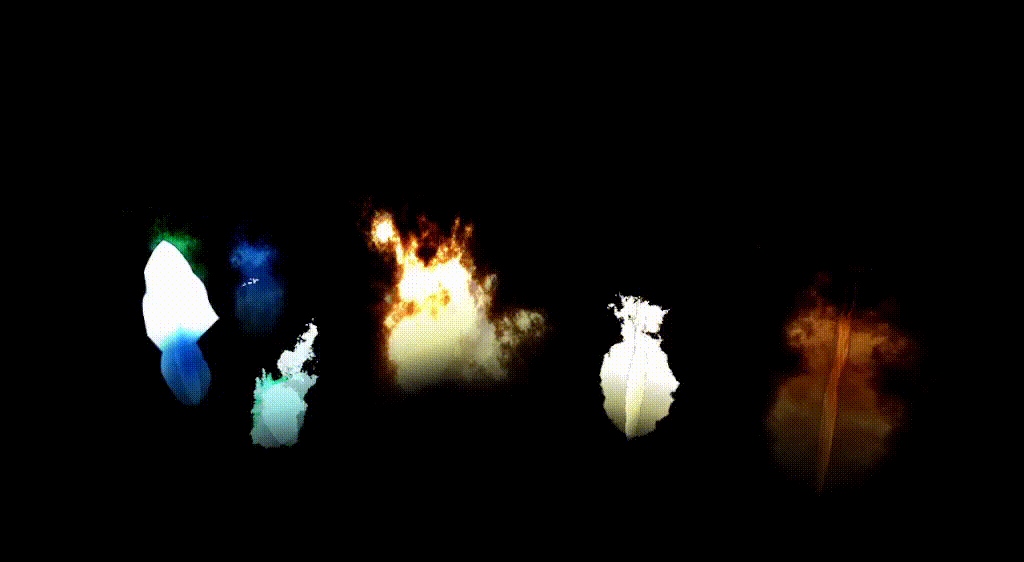
1. Terrain Generation in Games: Games like Minecraft use Perlin noise to procedurally generate vast, natural-looking terrains. In my post about marching cubes, I generated terrain using Perlin noise-based scalar field.
   • How: Perlin noise is used to simulate elevation. By controlling the frequency and scale of noise, different terrain types (hills, mountains, plains) can be generated seamlessly.
2. Cloud and Sky Textures: Many 3D applications and CGI use Perlin noise to generate clouds and fog, like those found in movies and weather simulations.
   • How: By layering multiple scales of Perlin noise (often called “fractal noise”), a natural cloud effect is created, with smooth transitions between light and dark areas.
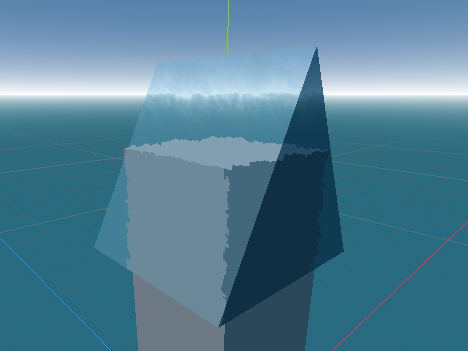
3. Simulating Water and Ocean Waves: In movies and games, Perlin noise can simulate the smooth, rolling effect of waves.
   • How: Noise values control the height and shape of waves across the water surface, with higher layers of noise simulating choppy waves and lower layers creating the rolling effect of the ocean. Typically, waves are calculated by wave functions and extra details are added using the noise functions; as in this godot ocean shader.
4. Fire and Smoke Effects: Perlin noise is used in particle systems to create realistic fire, smoke, and explosion effects in games and animation. It can also be used to add variations of color & intensity in fire shaders; like this godot fire shader.
   • How: Noise controls the density and transparency of particles, helping simulate the random but smooth behavior of smoke and flames.
5. Wood Grain and Marble Textures: Wood and marble textures for 3D objects in architecture and design.
   • How: Perlin noise values affect color variation and create grain patterns. For marble, multiple Perlin noise functions are combined with varying frequencies to simulate organic patterns.

Implementing Perlin Noise in GLSL

perlin noise can be made using python or other CPU side languages as well, but here I will show only GPU-side code in GLSL.

Defining the hash2d Function

The hash2d function generates random-looking gradient vectors for each grid point. It takes a 2D position and returns a 2D vector representing the gradient at that position. Here’s the GLSL code:

vec2 hash2d(vec2 position) {
    // Dot products to pseudo-randomize the input position
    position = vec2(
        dot(position, vec2(334.1, 781.7)),
        dot(position, vec2(652.5, 153.3))
    );
    
    // Calculate a "random" vector by using sin and fract functions
    return -1.0 + 3.0 * fract(sin(position) * 241.5453123);
}

Define the perlin Function

The perlin function computes the Perlin noise value for a given 2D position by:

• Calculating the four surrounding grid points
• Finding the distance of position from each corner
• Interpolating between the noise values from each corner smoothly

Here’s the GLSL code with a step-by-step explanation:

float perlin(vec2 position) {
    // Step 1: Get the grid cell's bottom-left corner
    vec2 i = floor(position);
    
    // Step 2: Find the relative position within the cell
    vec2 f = fract(position);
    
    // Step 3: Calculate the fade curve (using smooth interpolation)
    vec2 u = f * f * (3.0 - 2.0 * f);

    // Step 4: Compute dot products of each gradient with its distance vector
    float n00 = dot(hash2d(i + vec2(0.0, 0.0)), f - vec2(0.0, 0.0));
    float n10 = dot(hash2d(i + vec2(1.0, 0.0)), f - vec2(1.0, 0.0));
    float n01 = dot(hash2d(i + vec2(0.0, 1.0)), f - vec2(0.0, 1.0));
    float n11 = dot(hash2d(i + vec2(1.0, 1.0)), f - vec2(1.0, 1.0));

    // Step 5: Interpolate the results along x-axis
    float nx0 = mix(n00, n10, u.x);
    float nx1 = mix(n01, n11, u.x);

    // Step 6: Interpolate along y-axis and normalize the result
    return 0.5 + 0.5 * mix(nx0, nx1, u.y);
}

Visualize Perlin Noise in Shadertoy

This is step is only to show how the above functions will be called in shadertoy to visualize the shader. In reality, this part is different for different game engines. But here I am showing only for shadertoy.com.

In shadertoy shader, the main function is called mainImage. In mainImage, we use the perlin function to generate the noise and visualize it on the screen. We set up UV coordinates, scale them for zoom control, and then map the noise value to grayscale.

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
    // Normalize coordinates to the range [0,1]
    vec2 uv = fragCoord.xy / iResolution.y;
    
    // Scale UVs to zoom into the noise pattern
    uv *= 10.0;
    
    // Get Perlin noise value at the given UV coordinates
    float noiseValue = perlin(uv);
    
    // Map the noise value to a grayscale color and output
    fragColor = vec4(vec3(noiseValue), 1.0);
}

This shader will produce a smooth grayscale noise texture across the screen, with larger-scale patterns appearing due to the uv *= 10.0 scale factor. Adjust this factor to zoom in or out on the noise texture.

How it looks like:

Expanding the Perlin Noise Implementation

1. Adding multiple layers (octaves): Layering noise functions of different frequencies to create more complex patterns.
2. Applying it to different dimensions: Extending the method to 3D for volume textures, used in smoke or cloud simulations.
3. Modifying the gradient functions: Experimenting with gradient directions and fade functions for different artistic effects.

More Reading

1. The Book of Shaders: https://thebookofshaders.com/11/