Hydraulic erosion is a nature-based algorithm that simulates erosion caused by water on terrain. It is useful to make procedurally generated terrains look more realistic & interesting.
Hydraulic Erosion Overview
Water from mountains come down through slopes, forming creases along the way. This water is then accumulated as is travels, causing the formations of streams.
Along the whole path of water, it carries sediment & erodes the surface. This sediment is then deposited on lower elevations (plains).
Approaches
There are two common approaches:
1. Grid-based approach: For every vertex of the terrain, we keep track of water levels & pressures. In every iteration, we update new water levels based on pressures & as water moves, it carries the sediment along.
2. Particle-based approach: Here each particle (rain drop for example) is created at a random location which then flows on the terrain based on terrain’s normals or slope. It carries the sediment as it flows & deposits it to lower elevations.
Grid-based Algorithm for Erosion
This source discusses grid-based erosion technique and here is the paper.
Particle-based Algorithm for Erosion
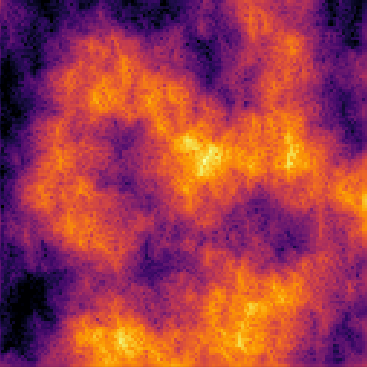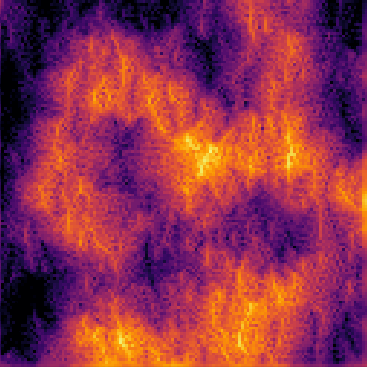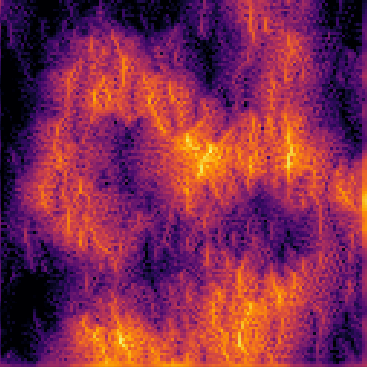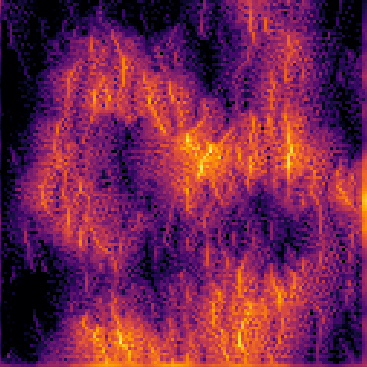
Pseudo-code
Below is the simplified pseudocode of the process. However, in implementation, we have many constant multipliers to fine-tune the output to look good; such as erosion rate, deposition rate, speed, etc.
sediment = 0
loop many_times:
normal = get normals at current position x, y
# if surface is flat, stop
if normal.up == 1: break
# the more the flat surface, the more the deposit
deposit = sediment * normal.up
# the more the slopy, the more the erosion
erosion = (1 - normal.up)
# the amount of deposit thrown at pos(x, y) and the amount of
# erosion stolen from pos(x, y). it is simply add the deposited
# and subtract the eroded dirt.
heightmap[x, y] -= (deposit - erosion)
sediment += (erosion - deposit)
# velocity is updated based on the slope
velocity.x = velocity.x + normal.x
velocity.y = velocity.y + normal.y
# position is updated based on velocity
old_position = current_position
current_position = current_position + velocity
# ! IMPORTANT: we erode terrain at old_position rather than
# ! current_position; otherwise, it causes digging of holesImplementation (Python)
Step 1: First, we need to represent our terrain in a convenient data structure. A heightmap is very efficient since it allows us to access the vertex position using array’s index values. If we need to access a vertex at vec2(5, 5), we only need to do something like heightmap[5][5] (gives height value h at this position). If you want to directly work on a 3D mesh, the problem is the mesh data structure stores vertices as a 1D array of vec3. So we will never know what index is the vertex vec3(5, 0, 5) lies on unless we search all the vertices.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.animation import FuncAnimation
from opensimplex import OpenSimplex
import math
# Heightmap size
width = 128
height = 128
"""
STEP 1: CREATE A HEIGHTMAP USING PERLIN NOISE
"""
def create_heightmap(width: int, height: int, scale: float = 32.0, seed: int = 42):
# Create a 2D array of floats
heightmap = np.zeros((width, height), dtype=float)
# Create a Perlin noise object
noise_generator = OpenSimplex(seed=seed)
# Generate Perlin noise and assign it to the heightmap
for i in range(height):
for j in range(width):
heightmap[i][j] = noise_generator.noise2(i / scale, j / scale)
heightmap[i][j] += noise_generator.noise2(i / scale / 2, j / scale / 2) * 0.5
heightmap[i][j] += noise_generator.noise2(i / (scale / 4), j / (scale / 4)) * 0.25
heightmap[i][j] += noise_generator.noise2(i / (scale / 8), j / (scale / 8)) * 0.125
heightmap[i][j] += noise_generator.noise2(i / (scale / 16), j / (scale / 16)) * 0.0625
heightmap[i][j] += noise_generator.noise2(i / (scale / 32), j / (scale / 32)) * 0.03125
# Normalize the heightmap to the range [0, 1]
heightmap -= heightmap.min()
heightmap /= heightmap.max()
return heightmap
heightmap = create_heightmap(width, height, seed=56456)Step 2: We should be able to calculate surface normals at any given position. The normal vector is later used to guide the water droplet’s motion. We calculate the normal vector on a particular position on heightmap using formula:
R, L, T, B are right, left, top, bottom neighbors of current position in heightmap
dx = (R - L) / 2
dy = (B - T) / 2
dz = -1
normal = vec3(dx, dy, dz).normalized()"""
STEP 2: GET THE 3D NORMAL VECTOR AT A SPECIFIC POSITION
"""
def get_normal(heightmap, position):
x, y = position
if x == 0 or x >= width-1 or y == 0 or y >= height-1:
return np.array([0, 0, 1], dtype=float)
R = heightmap[int(x+1), int(y)]
L = heightmap[int(x-1), int(y)]
T = heightmap[int(x), int(y+1)]
B = heightmap[int(x), int(y-1)]
dx = (R - L) * 0.5
dy = (B - T) * 0.5
dz = -1.0
normal = np.array([dx, dy, dz], dtype=float)
normal /= np.linalg.norm(normal)
return normal
# Get interpolated normals around the position - makes the normals a bit smoother
# though get_normal() is enough; but still...
def interpolated_normal(heightmap, position):
x, y = position
if x == 0 or x >= width-1 or y == 0 or y >= height-1:
return np.array([0, 0, 1], dtype=float)
R = get_normal(heightmap, [x+1, y])
L = get_normal(heightmap, [x-1, y])
T = get_normal(heightmap, [x, y+1])
B = get_normal(heightmap, [x, y-1])
TR = get_normal(heightmap, [x+1, y+1])
TL = get_normal(heightmap, [x-1, y+1])
BR = get_normal(heightmap, [x+1, y-1])
BL = get_normal(heightmap, [x-1, y-1])
return (R + L + T + B + TR + TL + BR + BL) / 8Step 3: To simulate erosion carried out by a single rain drop, we define some properties in Drop class. The actual algorithm lies here (see erode()). We will later spawn bunch of these drops to simulate erosion.
"""
STEP 3: MAKE A DROP CLASS FOR SIMULATION OF A SINGLE DROP
"""
class Drop:
velocity = np.array([0, 0], dtype=float)
old_position = np.array([0, 0], dtype=int)
current_position = np.array([0, 0], dtype=int)
sediment = 0.0
deposition_rate: float = 0.021 # const
erosion_rate: float = 0.051 # const
iteration_scale: float = 0.01 # const
friction: float = 0.01 # const
speed: float = 0.9910 # const
def __init__(self, position, velocity = np.array([0, 0], dtype=float)):
self.current_position = position
self.velocity = velocity
def erode(self, heightmap, max_iterations = 8):
for i in range(max_iterations):
normal = interpolated_normal(heightmap, self.current_position)
if normal[2] >= 0.9: break # If the terrain is flat, stop simulating (old: == 1)
deposit = self.sediment * self.deposition_rate * normal[2]
erosion = self.erosion_rate * (1 - normal[2]) * min(1, i * self.iteration_scale)
heightmap[int(self.old_position[0]), int(self.old_position[1])] -= (deposit - erosion)
self.sediment += (erosion - deposit)
self.velocity[0] = self.friction * self.velocity[0] + normal[0] * self.speed
self.velocity[1] = self.friction * self.velocity[1] + normal[1] * self.speed
self.old_position = self.current_position
self.current_position = self.current_position + self.velocityStep 4: Spawn many of these drops and simulate.
"""
STEP 4: SIMULATE EROSION USING MANY SUCH DROPS
"""
# Time to simulate
drops: int = 100000
def simulate():
for i in range(drops):
drop = Drop(np.array([np.random.randint(0, width), np.random.randint(0, height)], dtype=int))
drop.erode(heightmap)
simulate()Step 5: We can apply gaussian blur (optional) and finally display the eroded terrain using matplotlib in python.
"""
STEP 5: (OPTIONALLY) APPLY GAUSSIAN BLUR TO SMOOTHEN THE HEIGHTMAP
"""
def gaussian_blur(heightmap, radius):
kernel = np.array([[1, 2, 1], [2, 4, 2], [1, 2, 1]], dtype=float)
kernel /= np.sum(kernel)
for _ in range(radius):
heightmap = np.pad(heightmap, 1, mode='edge')
heightmap = np.array([[np.sum(heightmap[i:i+3, j:j+3] * kernel) for j in range(width)] for i in range(height)])
return heightmap
gaussian_blur(heightmap, 2)
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# Display 2D heightmap
plt.imshow(heightmap, cmap='inferno', interpolation='none')
plt.colorbar()
plt.show()
Complete Code
# Author: Mujtaba
# Date: Feb 10, 2024
# START -
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.animation import FuncAnimation
from opensimplex import OpenSimplex
import math
# Heightmap size
width = 128
height = 128
"""
STEP 1: CREATE A HEIGHTMAP USING PERLIN NOISE
"""
def create_heightmap(width: int, height: int, scale: float = 32.0, seed: int = 42):
# Create a 2D array of floats
heightmap = np.zeros((width, height), dtype=float)
# Create a Perlin noise object
noise_generator = OpenSimplex(seed=seed)
# Generate Perlin noise and assign it to the heightmap
for i in range(height):
for j in range(width):
heightmap[i][j] = noise_generator.noise2(i / scale, j / scale)
heightmap[i][j] += noise_generator.noise2(i / scale / 2, j / scale / 2) * 0.5
heightmap[i][j] += noise_generator.noise2(i / (scale / 4), j / (scale / 4)) * 0.25
heightmap[i][j] += noise_generator.noise2(i / (scale / 8), j / (scale / 8)) * 0.125
heightmap[i][j] += noise_generator.noise2(i / (scale / 16), j / (scale / 16)) * 0.0625
heightmap[i][j] += noise_generator.noise2(i / (scale / 32), j / (scale / 32)) * 0.03125
# Normalize the heightmap to the range [0, 1]
heightmap -= heightmap.min()
heightmap /= heightmap.max()
return heightmap
heightmap = create_heightmap(width, height, seed=56456)
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
"""
STEP 2: GET THE 3D NORMAL VECTOR AT A SPECIFIC POSITION
"""
def get_normal(heightmap, position):
x, y = position
if x == 0 or x >= width-1 or y == 0 or y >= height-1:
return np.array([0, 0, 1], dtype=float)
R = heightmap[int(x+1), int(y)]
L = heightmap[int(x-1), int(y)]
T = heightmap[int(x), int(y+1)]
B = heightmap[int(x), int(y-1)]
dx = (R - L) * 0.5
dy = (B - T) * 0.5
dz = -1.0
normal = np.array([dx, dy, dz], dtype=float)
normal /= np.linalg.norm(normal)
return normal
# Get interpolated normals around the position - makes the normals a bit smoother
# though get_normal() is enough; but still...
def interpolated_normal(heightmap, position):
x, y = position
if x == 0 or x >= width-1 or y == 0 or y >= height-1:
return np.array([0, 0, 1], dtype=float)
R = get_normal(heightmap, [x+1, y])
L = get_normal(heightmap, [x-1, y])
T = get_normal(heightmap, [x, y+1])
B = get_normal(heightmap, [x, y-1])
TR = get_normal(heightmap, [x+1, y+1])
TL = get_normal(heightmap, [x-1, y+1])
BR = get_normal(heightmap, [x+1, y-1])
BL = get_normal(heightmap, [x-1, y-1])
return (R + L + T + B + TR + TL + BR + BL) / 8
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
"""
STEP 3: MAKE A DROP CLASS FOR SIMULATION OF A SINGLE DROP
"""
class Drop:
velocity = np.array([0, 0], dtype=float)
old_position = np.array([0, 0], dtype=int)
current_position = np.array([0, 0], dtype=int)
sediment = 0.0
deposition_rate: float = 0.021 # const
erosion_rate: float = 0.051 # const
iteration_scale: float = 0.01 # const
friction: float = 0.01 # const
speed: float = 0.9910 # const
def __init__(self, position, velocity = np.array([0, 0], dtype=float)):
self.current_position = position
self.velocity = velocity
def erode(self, heightmap, max_iterations = 8):
for i in range(max_iterations):
normal = interpolated_normal(heightmap, self.current_position)
if normal[2] >= 0.9: break # If the terrain is flat, stop simulating (old: == 1)
deposit = self.sediment * self.deposition_rate * normal[2]
erosion = self.erosion_rate * (1 - normal[2]) * min(1, i * self.iteration_scale)
heightmap[int(self.old_position[0]), int(self.old_position[1])] -= (deposit - erosion)
self.sediment += (erosion - deposit)
self.velocity[0] = self.friction * self.velocity[0] + normal[0] * self.speed
self.velocity[1] = self.friction * self.velocity[1] + normal[1] * self.speed
self.old_position = self.current_position
self.current_position = self.current_position + self.velocity
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
"""
STEP 4: SIMULATE EROSION USING MANY SUCH DROPS
"""
# Time to simulate
drops: int = 100000
def simulate():
for i in range(drops):
drop = Drop(np.array([np.random.randint(0, width), np.random.randint(0, height)], dtype=int))
drop.erode(heightmap)
simulate()
"""
STEP 5: (OPTIONALLY) APPLY GAUSSIAN BLUR TO SMOOTHEN THE HEIGHTMAP
"""
def gaussian_blur(heightmap, radius):
kernel = np.array([[1, 2, 1], [2, 4, 2], [1, 2, 1]], dtype=float)
kernel /= np.sum(kernel)
for _ in range(radius):
heightmap = np.pad(heightmap, 1, mode='edge')
heightmap = np.array([[np.sum(heightmap[i:i+3, j:j+3] * kernel) for j in range(width)] for i in range(height)])
return heightmap
gaussian_blur(heightmap, 2)
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# Display 2D heightmap
plt.imshow(heightmap, cmap='inferno', interpolation='none')
plt.colorbar()
plt.show()
# - ENDMore reading
- https://www.firespark.de/resources/downloads/implementation%20of%20a%20methode%20for%20hydraulic%20erosion.pdf
- https://jobtalle.com/simulating_hydraulic_erosion.html
- https://nickmcd.me/2020/04/10/simple-particle-based-hydraulic-erosion/
- https://courses.grainger.illinois.edu/CS418/sp2023/text/erosion.html

